Abstract
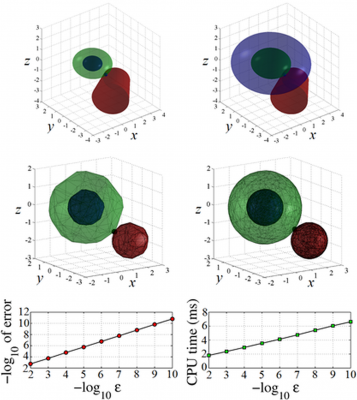
This paper presents an efficient algorithm for computing a distance measure between two compact convex sets Q and A, defined as the minimum scale factor such that the scaled Q is not disjoint from A. An important application of this algorithm in robotics is the computation of the minimum distance between two objects, which can be performed by taking A as the Minkowski difference of the objects and Q as a set containing the origin in its interior. In this generalized definition, the traditional Euclidean distance is a special case where Q is the unit ball. While this distance measure was proposed almost a decade ago, there has been no efficient algorithm to compute it in general cases. Our algorithm fills this void and we demonstrate its superior efficiency compared to approaches based on general-purpose optimization.
Copyright Notice
The documents contained in these directories are included by the contributing authors as a means to ensure timely dissemination of scholarly and technical work on a non-commercial basis. Copyright and all rights therein are maintained by the authors or by other copyright holders, notwithstanding that they have offered their works here electronically. It is understood that all persons copying this information will adhere to the terms and constraints invoked by each author’s copyright. These works may not be reposted without the explicit permission of the copyright holder.